

 |
 |
But a mathematician will undoubtedly conjure up the image of one of the most elegant geometric figures that exist! Here is a nice drawing of this 5-sided beauty.
Note that not only does it have 5 sides, but it also has 5 diagonals (AC, AD, BD, BE, CE). No other two-dimensional figure can claim that. Of course, as this is a regular pentagon, meaning all sides have equal length, all the diagonals have equal length as well.
Your task for this problem is to find the perimeter P and the area A, given that the length of any diagonal is
Hey, it's easier than it sounds. Just do a little background research on the properties of pentagons.
Extra: What is the perimeter and area of the little pentagon formed in the center of the star?
Say the word "pentagon" and different images will be called to mind, depending on who the listener may be. For example, an architect will probably think of the famous building in Washington, D.C. A politician will probably think about the collection of military persons that work in that building.

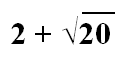
| Comments? Send e-mail. | Back to top | Go back to Home Page | Go back to Contents |