 |
LADDER
Math |
 |
This is a simple arithmetical activity, designed to give younger
students an introduction to a topic not normally encountered until high
school algebra, as least in a formal, abstract sense:
arithmetic sequences.
Here is how I present it to my students...
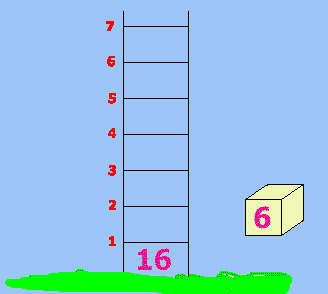
 Below you see a ladder standing up. The ladder has 7 rungs
(or steps). On the ground below the first rung is a number: 16.
Beside the ladder is a small box with the number 6 on it.
Below you see a ladder standing up. The ladder has 7 rungs
(or steps). On the ground below the first rung is a number: 16.
Beside the ladder is a small box with the number 6 on it.
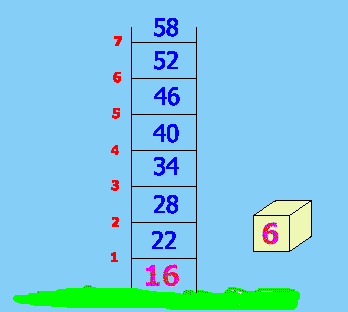
Your job is to put numbers on each of the seven rungs by
adding the box number over and over to the previous sum that you
obtain as you go up the ladder. This means: on the first rung you
will write 22 (because 22 = 16 + 6); then on the 2nd rung you will
write 28 (because 28 = 22 + 6); and so on.
When you have reached the 7th rung, your ladder picture
should look like this:
And that's all there is to it!
Well, not quite, actually...
You see there are four basic parts to each exercise in this
Ladder Math activity:
1. the ground number,
2. the box number,
3. the number of rungs of a ladder, and
4. the top, or final, number.
And this gives us four levels of difficulty, which I categorize
as follows:
1. Easy: when the top number is not known;
2. Medium: when the number of rungs is unknown;
3. Hard: when the ground number is missing; and
4. Hardest: when the box number is not given.
An example of each type is given in the chart below:
| Category |
Ground |
Box |
Rungs |
Top |
| Easy |
16 |
6 |
7 |
? |
| Medium |
20 |
9 |
? |
110 |
| Hard |
? |
8 |
8 |
94 |
| Hardest |
16 |
? |
7 |
93 |
 The example given above is obviously the one in the Easy
category. This type of exercise is therefore the basis on which this
activity is built. But when one of the other parts of information is
missing, things take on a different color.
The Medium category is actually rather easy as well. In it
one does not know just how many rungs the ladder should have prior
to doing the calculations. Once that is determined (in a rough draft
form), the drawing can then be sketched.
The example given above is obviously the one in the Easy
category. This type of exercise is therefore the basis on which this
activity is built. But when one of the other parts of information is
missing, things take on a different color.
The Medium category is actually rather easy as well. In it
one does not know just how many rungs the ladder should have prior
to doing the calculations. Once that is determined (in a rough draft
form), the drawing can then be sketched.
 More problem solving skills come into play, however, when an
exercise from the Hard category is attempted. (See the following
figure.)
More problem solving skills come into play, however, when an
exercise from the Hard category is attempted. (See the following
figure.)
For this one it is best to let the student work on it in any
way he/she wishes: (a) trial-and-check on the ground number; or (b)
using subtraction and working from "top down". Obviously, the latter
approach is more efficient and sophisticated, as it's a matter of
algebraic thinking, using inverse operations, etc. But it should not
be forced onto a student until he is ready for it.
 The highest degree of problem solving strategies come into
play when considering the Hardest category. Here the missing part
of information is the box number, the quantity that is to be added
each time. (See next figure.)
The highest degree of problem solving strategies come into
play when considering the Hardest category. Here the missing part
of information is the box number, the quantity that is to be added
each time. (See next figure.)
Undoubtedly, most students will experience some stress on this
one. Though the advanced math student knows the "shortcut" method,
or could soon figure it out, the novice would probably be obliged to
attack on the trial-and-check level. That in itself is a sign of
intelligent thinking.

Additional Comments and Extensions
With what has been presented here, you can clearly see how
to create more exercises for classroom use. But I would like to
suggest one particular idea. Since all the examples given above
dealt with positive integers (i.e. the simple counting numbers),
it would prove interesting to include one or two instances in which
"it doesn't come out, teacher!"
Depending on the maturity of the students, they may (1) give
up and just say "There is no answer.", or (2) try such things as
fractions or decimals. These days with calculators in general, and
fraction calculators in particular, this is an appropriate avenue to
explore.
Later, you can say up-front, "Some of these exercises need
to be solved using a box number that is fractional and/or decimal."
For example, here are some that use "nice" decimals and fractions:
1. ground = 15, box = (4.6), rungs = 5, top = 38
2. ground = 23, box = (2¾), rungs = 8, top = 45
 To summarize:
For a student who can discern patterns in work such as this,
a "formula" of sorts might be developed like this:
To summarize:
For a student who can discern patterns in work such as this,
a "formula" of sorts might be developed like this:
top = bottom + rungs × box
For the student of advanced algebra, the textbook formula for
this work might be given as follows:
an = a1 + (n - 1)d
where an = the nth term,
a1 = the first term,
n = the number of terms being considered, and
d = the "common difference", i.e. the value
being added each time.