
 |
Preface: On this page I present a series of three handout sheets that I use in my Pre-algebra classes whose purpose is to teach how to find out if a large number is a prime or not. And by "large", my main concern, as you will soon see, are numbers greater than 100 and less than 10,000. It is a bit lengthy, but it was designed to make certain the students have a firm grasp on the important background concepts necessary to deal with the work to be done in the whole activity. And it is presumed before seeing this material that the student already knows what a prime number is. My prefered definition is: a whole number, greater than one, whose only factors are itself and one.
1. Square root: the square root of a number is a value which when
multiplied by itself produces the given number. Examples:
4 is the square root of 16 because 4 × 4 = 16;
15 is the square root of 225 because 15 × 15 = 225; and
38 is the square root of 1444 because 38 × 38 = 1444.
2. Often a number does not have a whole number square root like the
three examples above. For instance, there are no whole numbers
such that when multiplied by themselves will give us 20, 85, or 150.
For 20, 4 × 4 = 16 is too small; and 5 × 5 = 25 is too big.
For 85, 9 × 9 = 81 is too small; and 10 × 10 = 100 is too big.
For 150, 12 × 12 = 144 is too small; and 13 × 13 = 169 is too big.
3. But by using decimals, we can get closer to the numbers. Observe:
For 20, 4.4 × 4.4 = 19.36 and 4.5 × 4.5 = 20.25 are better choices.
For 85, 9.2 × 9.2 = 84.64 and 9.3 × 9.3 = 86.49 are better choices.
For 150, 12.2 × 12.2 = 148.84 and 12.3 × 12.3 = 151.29 are better
choices.
4. Our calculator can help us find these decimal values more rapidly
than mere guessing. There is a key with a symbol like this: √.
Pressing it after entering your number (on most calculator models)
will give you an approximation of several digits.
For 20, we obtain 4.472135955.
For 85, we obtain 9.219544457.
For 150, we obtain 12.2474487.
Remember: these are just approximations. Unless a number is
the square of a whole number to begin with, the square root can only
be "more or less" good.
5. Just as finding the square of a number -- using the calculator key
identified as x2 -- is a very important idea in mathematics, so is
finding the square root of a number. While the ideas are related, they
are very different; so be careful how you use them.
The square root of 16 is 4; but the square of 16 is 256.

BIG PRIMES
Background: II
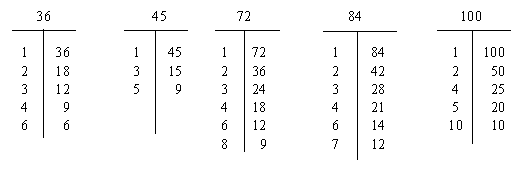
6. Earlier in your math study you learned how to make factor charts.
Here are some examples to refresh your memory.

BIG PRIMES
The Lesson
1. Let's begin with an example done step-by-step.
Is 2111 a prime or not?
- testing a given set of numbers to see if they are prime or not;
- ask students to find 5 or 6 primes in this range of their own choice, providing the charts to support the results;
- make a contest to see who can find the most primes, say from 1000 to 2000, for homework.
When I make a little quiz on this, I use about five numbers, two of which are prime and the rest are not -- just to keep things honest. In the final analysis, I feel this work makes a "good problem" that takes more than just a minute or so to do, involves important number theoretic ideas, and is made feasible by the intelligent use of the calculator.
In Part II, mention was made about memorizing the primes from 1 to 100. This is not as great a task as it may sound at first. There are only 25 of them, ten of which are less than 30. And when one knows the divisibility tests for 2, 3, 5, and 7, the memorization is virtually automatic. To ease the task, the 25 primes can be grouped like this:
2, 3, 5, 7 53, 59 11, 13, 17, 19 61, 67 23, 29 71, 73, 79 31, 37 83, 89 41, 43, 47 97

Researchers Discover Largest Multi-Million-Digit Prime
Using Entropia Distributed Computing Grid.
213,466,917 - 1 is now the Largest Known Prime.
For more information, click http://www.mersenne.org/13466917.htm.
| Comments? Send e-mail. | Back to top | Go back to Home Page | Go back to Contents |