&
284

| 220 & 284 |
 |
[Note: In another article we presented the concept of Perfect Numbers, and the related two classes of numbers, Deficient and Abundant. If you have not read that one, it would be a good idea to do so now before proceeding here. The topic before us now is a natural extension of that article.]
For centuries men have felt that numbers had powers over the natural affairs of their lives. One small piece of evidence of this concept is that of Amicable, or Friendly, Numbers. These are merely pairs of numbers that are connected in a special way. The math behind the relationship is the same that was used to classify numbers as either perfect, deficient, or abundant: the sum of the proper divisors of the number, or numbers, being considered. An example will make this clear:
The number pair of 220 and 284 are considered amicable, because the sum of the proper divisors of 220 is 284, while the sum of the proper divisors of 284 is 220. Got that? Look at these factor charts:
220 284 ---|---- ---|---- 1 | 1 | 2 | 110 2 | 142 4 | 55 4 | 71 5 | 44 10 | 22 11 | 20 [NOTE: In this sort of work, divisor and factor are synonyms.]
The sum of the divisors in the larger chart {1, 2, 4, 5, 10, ... , 110} is equal to the other number (284), whereas the sum of the divisors in the smaller chart {1, 2, 4, 71, 142} is the first number (220).
Nice, huh!
I have read that in times long ago when romantic love was, well, more cerebral than material, amicable numbers were used by a young man to express his love to his beloved. He would prepare two metal charms with the numbers 220 and 284 engraved on them. These were then put on chains to place around their necks. Maybe we should do it these days, too.
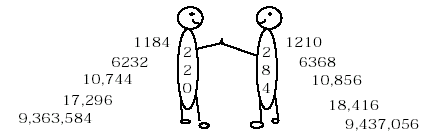
Just as mathematicians have searched long and hard to find perfect numbers, they have done the same for amicable ones. And as you might expect, the sizes of the numbers soon become very large. (Some are so large that if a lover used them to make a love token, the charm would be a "back breaking" burden for the wearer.)
About 1200 pairs are known by the last count that I have access to.* Here are the smaller members of two different pairs: 2620 and 5020. I leave it as "homework" for you to find the partners that apply to each of them.
But there is one pair that mathematicians missed in their search down through the centuries which was found by an Italian schoolboy in the last century. One number of the pair is 1184. We leave it to you, dear reader, to find its "loving" companion. [Hint: look in the cartoon above.]
| Comments? Send e-mail. | Back to top | Go back to Home Page | Go back to Contents |